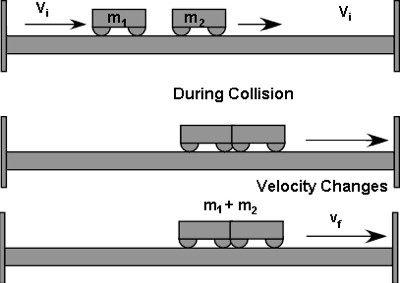
Inelastic Collision can only be solved from the "before clause" ( mass of object 1 multiplied by its velocity + mass of object 2 multiplied by its velocity) equaling the "after clause" (both masses added multiplied by the final velocity).

1. A 15-kg medicine ball is thrown at a velocity of 20 km/hr to a 60-kg person who is at rest on ice. The person catches the ball and subsequently slides with the ball across the ice. Determine the velocity of the person and the ball after the collision.

2. A 0.150-kg baseball moving at a speed of 45.0 m/s crosses the plate and strikes the 0.250-kg catcher's mitt (originally at rest). The catcher's mitt immediately recoils backwards (at the same speed as the ball) before the catcher applies an external force to stop its momentum. If the catcher's hand is in a relaxed state at the time of the collision, it can be assumed that no net external force exists and the law of momentum conservation applies to the baseball-catcher's mitt collision. Determine the post-collision velocity of the mitt and ball.

3. Two gumballs, of mass m and mass 2m respectively, collide head-on. Before impact, the gumball of mass m is moving with a velocity , and the gumball of mass 2m is stationary. What is the final velocity, , of the gumball wad?

4. Two balls, each with mass 2 kg, and velocities of 2 m/s and 3 m/s collide head on. Their final velocities are 2 m/s and 1 m/s, respectively. Is this elastic or Inelastic?

5. A car of 500 kg, traveling at 30 m/s rear ends another car of 600 kg, traveling at 20 m/s. in the same direction The collision is great enough that the two cars stick together after they collide. How fast will both cars be going after the collision?

Inelastic Collision: Math Problems

m1v1 + m2v2= (m1 + m2)v

OR